
Breaking News
6.5x55 Swedish vs. 6.5 Creedmoor: The New 6.5mm Hotness
Best 7mm PRC Ammo: Hunting and Long-Distance Target Shooting
 Christmas Truce of 1914, World War I - For Sharing, For Peace
Christmas Truce of 1914, World War I - For Sharing, For Peace
Top Tech News
 EngineAI T800: Born to Disrupt! #EngineAI #robotics #newtechnology #newproduct
EngineAI T800: Born to Disrupt! #EngineAI #robotics #newtechnology #newproduct
 This Silicon Anode Breakthrough Could Mark A Turning Point For EV Batteries [Update]
This Silicon Anode Breakthrough Could Mark A Turning Point For EV Batteries [Update]
 Travel gadget promises to dry and iron your clothes – totally hands-free
Travel gadget promises to dry and iron your clothes – totally hands-free
 Perfect Aircrete, Kitchen Ingredients.
Perfect Aircrete, Kitchen Ingredients.
 Futuristic pixel-raising display lets you feel what's onscreen
Futuristic pixel-raising display lets you feel what's onscreen
 Cutting-Edge Facility Generates Pure Water and Hydrogen Fuel from Seawater for Mere Pennies
Cutting-Edge Facility Generates Pure Water and Hydrogen Fuel from Seawater for Mere Pennies
 This tiny dev board is packed with features for ambitious makers
This tiny dev board is packed with features for ambitious makers
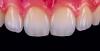 Scientists Discover Gel to Regrow Tooth Enamel
Scientists Discover Gel to Regrow Tooth Enamel
 Vitamin C and Dandelion Root Killing Cancer Cells -- as Former CDC Director Calls for COVID-19...
Vitamin C and Dandelion Root Killing Cancer Cells -- as Former CDC Director Calls for COVID-19...
 Galactic Brain: US firm plans space-based data centers, power grid to challenge China
Galactic Brain: US firm plans space-based data centers, power grid to challenge China
New type of supercomputer could be based on 'magic dust' combination of light and matter
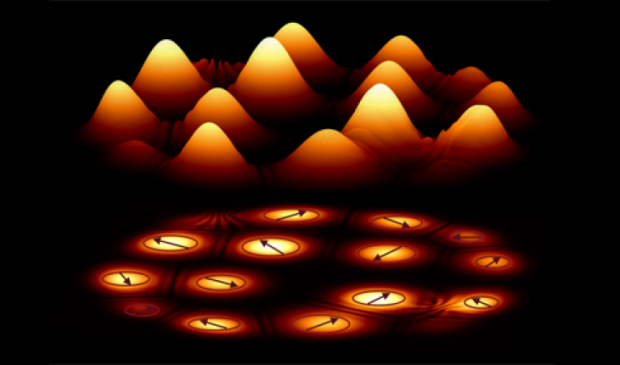
The researchers, from Cambridge, Southampton and Cardiff Universities in the UK and the Skolkovo Institute of Science and Technology in Russia, have used quantum particles known as polaritons – which are half light and half matter – to act as a type of 'beacon' showing the way to the simplest solution to complex problems. This entirely new design could form the basis of a new type of computer that can solve problems that are currently unsolvable, in diverse fields such as biology, finance or space travel. The results are reported in the journal Nature Materials.
Our technological progress — from modelling protein folding and behaviour of financial markets to devising new materials and sending fully automated missions into deep space — depends on our ability to find the optimal solution of a mathematical formulation of a problem: the absolute minimum number of steps that it takes to solve that problem.
The search for an optimal solution is analogous to looking for the lowest point in a mountainous terrain with many valleys, trenches, and drops. A hiker may go downhill and think that they have reached the lowest point of the entire landscape, but there may be a deeper drop just behind the next mountain. Such a search may seem daunting in natural terrain, but imagine its complexity in high-dimensional space.

 The State's Last Stand
The State's Last Stand


