
Breaking News
 Iran Regime Kills Protesters as Unrest and Calls for Regime Change Spread Nationwide
Iran Regime Kills Protesters as Unrest and Calls for Regime Change Spread Nationwide
 Trump, Treason, and the New York Times
Trump, Treason, and the New York Times
 Democrat idiocy at work in San Francisco
Democrat idiocy at work in San Francisco
 BREAKING THROUGH Tesla AI in 2026
BREAKING THROUGH Tesla AI in 2026
Top Tech News
 Laser weapons go mobile on US Army small vehicles
Laser weapons go mobile on US Army small vehicles
 EngineAI T800: Born to Disrupt! #EngineAI #robotics #newtechnology #newproduct
EngineAI T800: Born to Disrupt! #EngineAI #robotics #newtechnology #newproduct
 This Silicon Anode Breakthrough Could Mark A Turning Point For EV Batteries [Update]
This Silicon Anode Breakthrough Could Mark A Turning Point For EV Batteries [Update]
 Travel gadget promises to dry and iron your clothes – totally hands-free
Travel gadget promises to dry and iron your clothes – totally hands-free
 Perfect Aircrete, Kitchen Ingredients.
Perfect Aircrete, Kitchen Ingredients.
 Futuristic pixel-raising display lets you feel what's onscreen
Futuristic pixel-raising display lets you feel what's onscreen
 Cutting-Edge Facility Generates Pure Water and Hydrogen Fuel from Seawater for Mere Pennies
Cutting-Edge Facility Generates Pure Water and Hydrogen Fuel from Seawater for Mere Pennies
 This tiny dev board is packed with features for ambitious makers
This tiny dev board is packed with features for ambitious makers
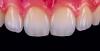 Scientists Discover Gel to Regrow Tooth Enamel
Scientists Discover Gel to Regrow Tooth Enamel
 Vitamin C and Dandelion Root Killing Cancer Cells -- as Former CDC Director Calls for COVID-19...
Vitamin C and Dandelion Root Killing Cancer Cells -- as Former CDC Director Calls for COVID-19...
Race to Quantum Computing Supremacy should see definitive results in 2018

A critical question for the field of quantum computing in the near future is whether quantum devices without error correction can perform a well-defined computational task beyond the capabilities of state-of-the-art classical computers, achieving so-called quantum supremacy. We study the task of sampling from the output distributions of (pseudo-)random quantum circuits, a natural task for benchmarking quantum computers.
Crucially, sampling this distribution classically requires a direct numerical simulation of the circuit, with computational cost exponential in the number of qubits. This requirement is typical of chaotic systems. We extend previous results in computational complexity to argue more formally that this sampling task must take exponential time in a classical computer.
We study the convergence to the chaotic regime using extensive supercomputer simulations, modeling circuits with up to 42 qubits - the largest quantum circuits simulated to date for a computational task that approaches quantum supremacy. We argue that while chaotic states are extremely sensitive to errors, quantum supremacy can be achieved in the near-term with approximately fifty superconducting qubits.



