
Breaking News
 Christmas Truce of 1914, World War I - For Sharing, For Peace
Christmas Truce of 1914, World War I - For Sharing, For Peace
 The Roots of Collectivist Thinking
The Roots of Collectivist Thinking
 What Would Happen if a Major Bank Collapsed Tomorrow?
What Would Happen if a Major Bank Collapsed Tomorrow?
Top Tech News
 Travel gadget promises to dry and iron your clothes – totally hands-free
Travel gadget promises to dry and iron your clothes – totally hands-free
 Perfect Aircrete, Kitchen Ingredients.
Perfect Aircrete, Kitchen Ingredients.
 Futuristic pixel-raising display lets you feel what's onscreen
Futuristic pixel-raising display lets you feel what's onscreen
 Cutting-Edge Facility Generates Pure Water and Hydrogen Fuel from Seawater for Mere Pennies
Cutting-Edge Facility Generates Pure Water and Hydrogen Fuel from Seawater for Mere Pennies
 This tiny dev board is packed with features for ambitious makers
This tiny dev board is packed with features for ambitious makers
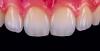 Scientists Discover Gel to Regrow Tooth Enamel
Scientists Discover Gel to Regrow Tooth Enamel
 Vitamin C and Dandelion Root Killing Cancer Cells -- as Former CDC Director Calls for COVID-19...
Vitamin C and Dandelion Root Killing Cancer Cells -- as Former CDC Director Calls for COVID-19...
 Galactic Brain: US firm plans space-based data centers, power grid to challenge China
Galactic Brain: US firm plans space-based data centers, power grid to challenge China
 A microbial cleanup for glyphosate just earned a patent. Here's why that matters
A microbial cleanup for glyphosate just earned a patent. Here's why that matters
 Japan Breaks Internet Speed Record with 5 Million Times Faster Data Transfer
Japan Breaks Internet Speed Record with 5 Million Times Faster Data Transfer
Rigetti has a 19 qubit quantum computing system and it runs unsupervised machine learning

Arxiv – Unsupervised Machine Learning on a Hybrid Quantum Computer
Machine learning techniques have led to broad adoption of a statistical model of computing. The statistical distributions natively available on quantum processors are a superset of those available classically. Harnessing this attribute has the potential to accelerate or otherwise improve machine learning relative to purely classical performance. A key challenge toward that goal is learning to hybridize classical computing resources and traditional learning techniques with the emerging capabilities of general purpose quantum processors. Here, we demonstrate such hybridization by training a 19-qubit gate model processor to solve a clustering problem, a foundational challenge in unsupervised learning. We use the quantum approximate optimization algorithm in conjunction with a gradient-free Bayesian optimization to train the quantum machine. This quantum/classical hybrid algorithm shows robustness to realistic noise, and we find evidence that classical optimization can be used to train around both coherent and incoherent imperfections.

 The State's Last Stand
The State's Last Stand


