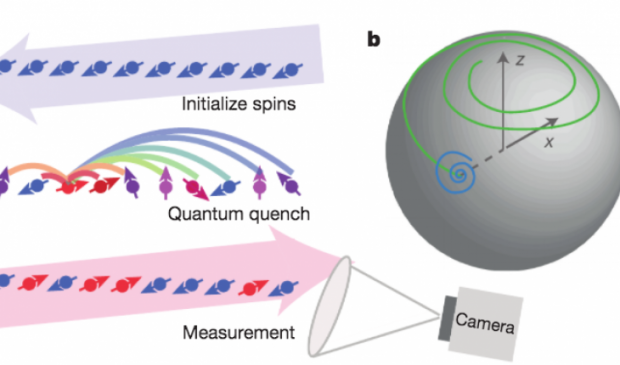
This experimental platform can be extended to tackle provably hard quantum problems such as Ising sampling. Given an even higher level of control over the interactions between spins, as already demonstrated for smaller numbers of trapped-ion qubits, this same system can be upgraded to a universal quantum computer.

Nature – Observation of a many-body dynamical phase transition with a 53-qubit quantum simulator

A quantum simulator is a type of quantum computer that controls the interactions between quantum bits (or qubits) in a way that can be mapped to certain quantum many-body problems. As it becomes possible to exert more control over larger numbers of qubits, such simulators will be able to tackle a wider range of problems, such as materials design and molecular modeling, with the ultimate limit being a universal quantum computer that can solve general classes of hard problems3. Here we use a quantum simulator composed of up to 53 qubits to study non-equilibrium dynamics in the transverse-field Ising model with long-range interactions. We observe a dynamical phase transition after a sudden change of the Hamiltonian, in a regime in which conventional statistical mechanics does not apply. The qubits are represented by the spins of trapped ions, which can be prepared in various initial pure states. We apply a global long-range Ising interaction with controllable strength and range, and measure each individual qubit with an efficiency of nearly 99 per cent. Such high efficiency means that arbitrary many-body correlations between qubits can be measured in a single shot, enabling the dynamical phase transition to be probed directly and revealing computationally intractable features that rely on the long-range interactions and high connectivity between qubits.