
Breaking News
 The Tenpenny Files with Patrick Byrne
The Tenpenny Files with Patrick Byrne
 What Just Happened With Ron Paul Changes EVERYTHING (You're Witnessing History)
What Just Happened With Ron Paul Changes EVERYTHING (You're Witnessing History)
 Piers Morgan CLASHES with Candace Owens During On-Air Firestorm Interview:
Piers Morgan CLASHES with Candace Owens During On-Air Firestorm Interview:
 House Passes Bill to Prosecute Doctors and Parents for Sex Changes for Children...
House Passes Bill to Prosecute Doctors and Parents for Sex Changes for Children...
Top Tech News
 This tiny dev board is packed with features for ambitious makers
This tiny dev board is packed with features for ambitious makers
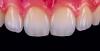 Scientists Discover Gel to Regrow Tooth Enamel
Scientists Discover Gel to Regrow Tooth Enamel
 Vitamin C and Dandelion Root Killing Cancer Cells -- as Former CDC Director Calls for COVID-19...
Vitamin C and Dandelion Root Killing Cancer Cells -- as Former CDC Director Calls for COVID-19...
 Galactic Brain: US firm plans space-based data centers, power grid to challenge China
Galactic Brain: US firm plans space-based data centers, power grid to challenge China
 A microbial cleanup for glyphosate just earned a patent. Here's why that matters
A microbial cleanup for glyphosate just earned a patent. Here's why that matters
 Japan Breaks Internet Speed Record with 5 Million Times Faster Data Transfer
Japan Breaks Internet Speed Record with 5 Million Times Faster Data Transfer
 Advanced Propulsion Resources Part 1 of 2
Advanced Propulsion Resources Part 1 of 2
 PulsarFusion a forward-thinking UK aerospace company, is pushing the boundaries of space travel...
PulsarFusion a forward-thinking UK aerospace company, is pushing the boundaries of space travel...
 Dinky little laser box throws big-screen entertainment from inches away
Dinky little laser box throws big-screen entertainment from inches away
 'World's first' sodium-ion flashlight shines bright even at -40 ºF
'World's first' sodium-ion flashlight shines bright even at -40 ºF
Ultimate Photonic Rocket

Haug has recently introduced a new maximum velocity for subatomic particles (anything with rest mass) that is just below the speed of light. This is combined with the relativistic rocket equation in order to assess how much fuel would be needed to accelerate an ideal particle rocket to its maximum velocity.
Planck masses of fuel 4.35302 × 10−08 kg.
Max speed for an electron 99.9999999999999999999999999999999999999999999124% of the speed of light
Max speed for a proton 99.999999999999999999999999999999999999705 of the speed of light
The maximum amount of fuel needed for any fully-efficient particle rocket is equal to two Planck masses. This amount of fuel will bring any subatomic particle up to its maximum velocity. At this maximum velocity the subatomic particle will itself turn into a Planck mass particle and likely will explode into energy. Interestingly, we need no fuel to accelerate a fundamental particle that has a rest-mass equal to Planck mass up to its maximum velocity. This is because the maximum velocity of a Planck mass particle is zero as observed from any reference frame. However, the Planck mass particle can only be at rest for an instant. The Planck mass particle can be seen as the very turning point of two light particles; it exists when two light particles collide. Haug's newly-introduced maximum mass velocity equation seems to be fully consistent with application to the relativistic rocket equation and it gives an important new insight into the ultimate limit of fully-efficient particle rockets.



